
1. 벡터의 외적 : cross product
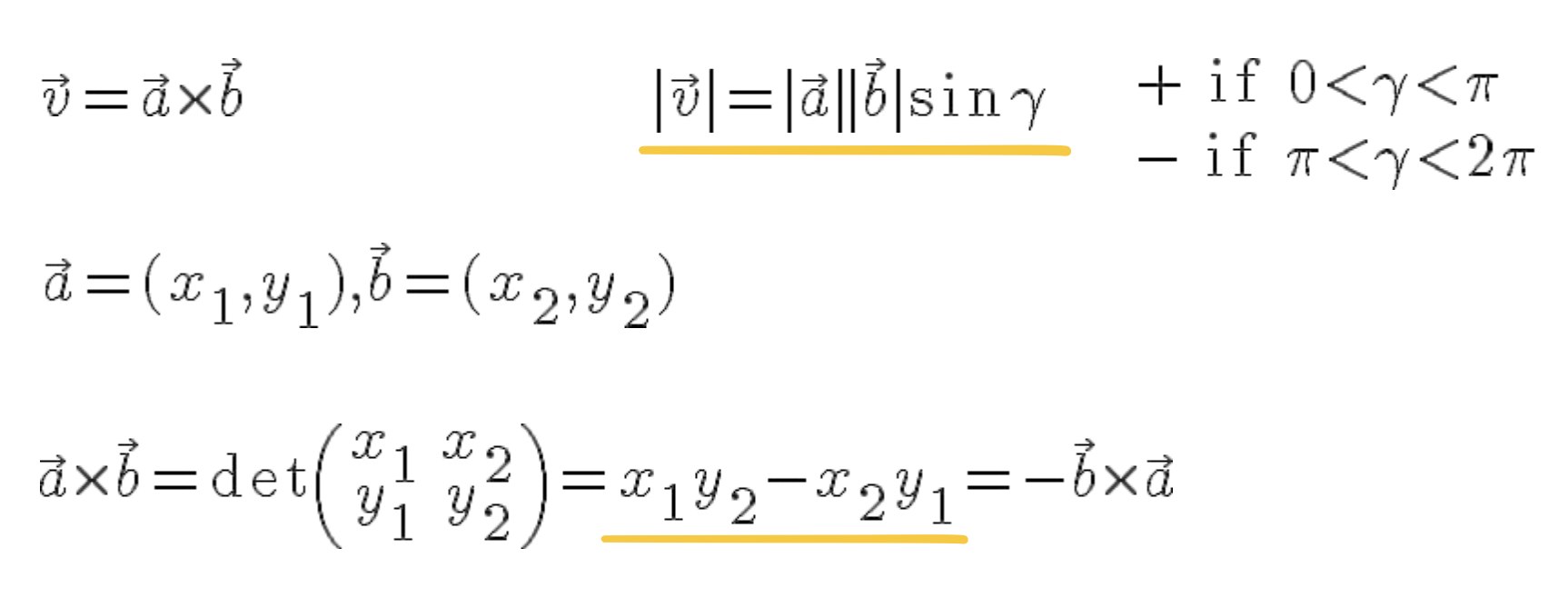
2. 외적의 응용 : 부호 점검
3. CCW 알고리즘 : Counter-Clock Wise
세 점이 주어졌을 때 A->B와 A->C 두 벡터의 외적의 부호가 방향을 결정함.
int ccw(int x1, int y1, int x2, int y2, int x3, int y3){
int tmp = x1*y2 + x2*y3 + x3*y1;
tmp -= (y1*x2 + y2*x3 + y3*x1);
if(tmp > 0) return 1; // a에 대해 b가 반시계 방향(왼쪽)에 있음
else if(tmp < 0) return -1; // a에 대해 b가 시계 방향(오른쪽)에 있음
else return 0;
}
4. 응용 : 선분의 교차 여부
a-b를 이은 벡터 A에 대해 a-c와 a-d가 반대 방향이면 벡터 A와 c-d는 교차한다.
5. 선분의 교차를 푸는 무식한 방법
- 두 선분을 직선으로 보고 교점을 찾기
- 교점이 두 선분 위에 있는지 확인
시간이 많이 소요, 정수가 아닌 실수 연산으로 인한 오차 발생 가능성 (나눗셈 할 때 문제 발생)

6. 외적을 이용한 선분 교차 판정 : 두 선분 모두의 입장에서 점검한다
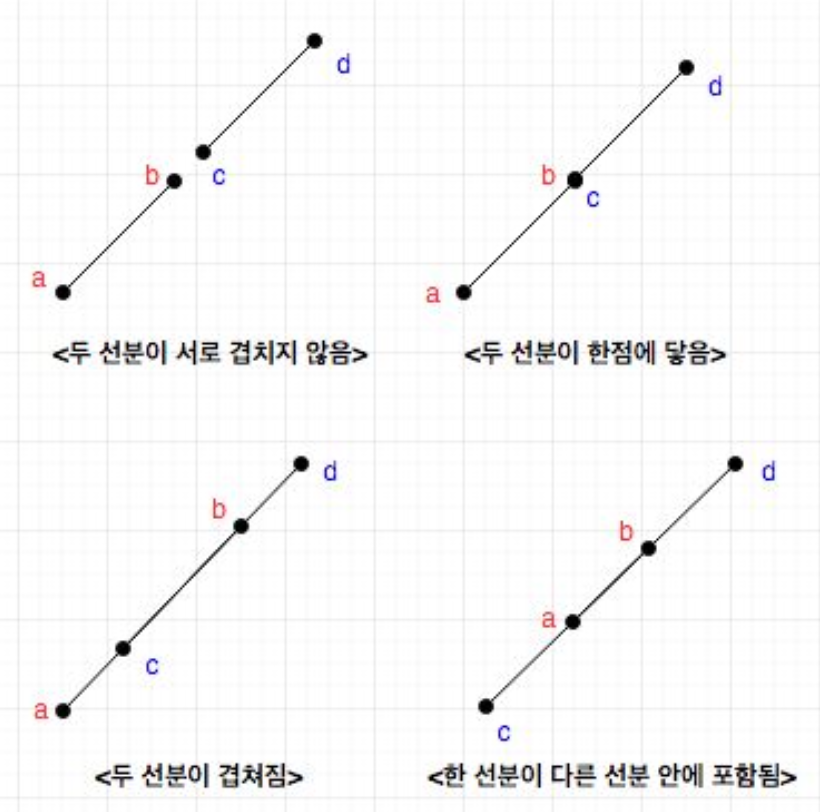
예외사항) 두 선분이 겹치지 않을때(만나지 않을때), 두 선분의 끝이 만날 때, 두 선분이 겹쳐질때, 한 선분이 다른선분에 포함될 떄
CCW 알고리즘은 위 4가지 경우에 모두 거짓이다.
-> 외적이 0이 된다면 교점을 구하여 점검하기!!
1차원 직선 상에서 선분 [a, b]는 양 끝점이 좌표 a, b인 점이고 [c, d]도 마찬가지입니다.
인생을 편하게 하기 위해서 a <= b, c <= d라고 가정합시다.
left = min(a, c), right = max(b, d)
- 두 선분이 만나지 않는다 : a, b, c, d의 위치관계를 생각해보면 좀 복잡합니다.
a <= b < c <= d 또는 c <= d < a <= b 라면 만나지 않겠죠.
약간만 생각하면, right - left > |b-a| + |d - c| 임을 알 수 있습니다. 두 선분의 길이의 합이 가장 왼쪽 끝점과 가장 오른쪽 끝점을 잇는 선분의 길이보다 짧은 것이죠.
비슷하게,
- 두 선분이 한 점에서 만난다 :
a <= b = c <= d 또는 c <= d = a <= b이지만
right - left = |b - a| + |d - c|
- 두 선분이 교차한다 :
right - left < |b - a| + |d - c|
- 한 선분이 두 선분 안에 완전히 포함된다:
rifht - left = |b - a| or |d - c|
7. 두 수의 최대 공약수 찾기 : 유클리드 알고리즘 (Euclid)
GCD(a,b) = GCD(b, a-b)
why? a=a'g, b=b'g -> b-a = (b' - a')g
O( log max(a,b) ) -> 소인수분해보다 빠름.
최악의 상황 : 피보나치 숫자
ax+by = GCD(a,b)
unsigned int gcd(unsigned int a, unsigned int b){
if(a<b) return gcd(b,a);
if(b==0) return a;
return gcd(b, a - b); // 뺄셈
}
// 더 빠른 gcd
unsigned int gcd(unsigned int a, unsigned int b){
if(a<b) return gcd(b,a);
if(b==0) return a;
return gcd(b, a % b); // 나머지 연산
}
~ 인복 말씀 ~
GCD(23, 5) = GCD(5, 3)
3 = 23*1 - 5*4
GCD(5, 3) = GCD(3, 2)
2 = 5 - 3 = 5 - (23*1 - 5*4) = 5*5 - 23*1
GCD(3, 2) = GCD(2, 1) = GCD(1, 0)
1 = 3 - 2 = (23*1 - 5*4) - (5*5 - 23*1)
= 23*2 - 5*9
정리 1. GCD(a, b)를 유클리드 알고리즘으로 구하는 과정에서 GCD를 구하는 두 수는 항상 ax+by꼴이다.
(= 결국 이 중 하나가 GCD(a, b)이기 때문에 GCD(a, b) = ax+by가 되는 x, y가 존재한다)
증명. 수학적 귀납법.
기본) a = a*1 + b*0, b = a*0 + b*1
귀납) GCD(ax + by, a'x + b'y)를 구할 때 ax + by > a'x + b'y라고 가정하면
GCD(ax + by, a'x + b'y) = GCD(a'x + b'y, ((ax+by) - (a'x+b'y))
= GCD(a'x + b'y, (a-a')x + (b-b')y) 이므로 항상 성립한다.
8. 유한체 : Finite Field
자연수를 소수 p로 나눈 나머지의 집합 Z = {0,1,...,p-1}
이 집합에서 덧셈, 뺄셈, 곱셈을 정의 가능하다.
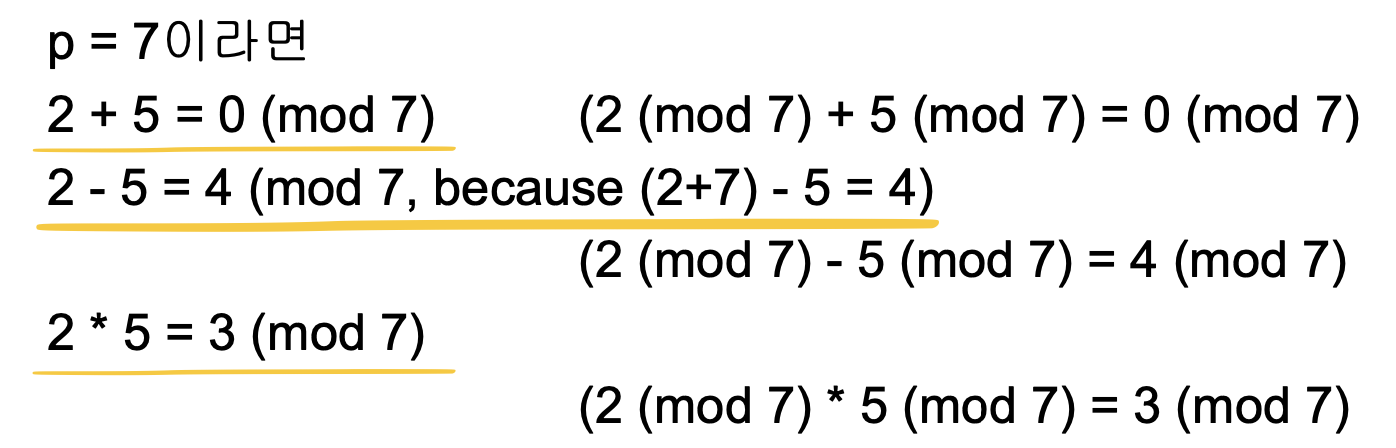
나눗셈은? -> 곱셈이 성립한다는 조건을 활용
곱셈에 대한 항등원은 1이므로, 나눗셈은 곱해서 1이 되는 수를 찾는 과정이다 (곱셈의 역원)
a * x = 1 (mod p)
9. 위 식에서 x를 구하는 것이 확장 유클리드 알고리즘이다
서로소인 p와 a가 주어졌을 때, ab = 1 (mod p) 의 b를 구하시오.
-> GCD(a,p) = ax + py 인 x, y가 존재하며, 이 값은 a와 p가 서로소이므로 1이다.
따라서 GCD(a,p) = 1을 구하는 과정에서 이 조건을 만족하는 x를 구할 수 있다.
a=4, p=7이라고 하면
GCD(4,7) = GCD(4, 7-4) = GCD(7-4, 4-(7-4)) = GCD(4-(7-4), (7-4)%(4-(7-4))) = 1
이 식 중에서 4-(7-4) = 4 + 4 - 7 = 4*2 - 7*1 = 1 이므로, b = 2
10. Extended Euclidean Algorithm
#include <iostream>
using namespace std;
int xGCD(int a, int b, int &x, int &y){
if(b==0) {
cout << x << " " << y << "\n";
return a;
}
cout << x << " " << y << "\n";
int x1, y1;
x1 = y;
y1 = x - (a / b) * y;
int gcd = xGCD(b, a % b, x1, y1);
return gcd;
}
int main(){
int x = 1;
int y = 0;
cout << xGCD(4, 7, x, y);
}
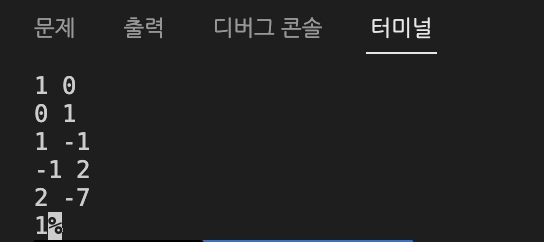
여기서
x1 = y;
y1 = x - (a / b) * y;
이 식이 나온 이유는, gcd(a, b) = gcd(b, a%b) 에서
bx + (a%b)y = bx + (a - (a/b)*b)y = ay + b(x - (a/b)y) 이렇게 정리되기 때문이다.
그래서 새로운 x1에 y가 들어가고, 새로운 y1에 x - (a/b) * y 가 대입되는 것이다.
'📚 전공 공부 > 문제해결기법' 카테고리의 다른 글
| [문제해결기법] 6. 세그먼트 트리 (0) | 2023.04.18 |
|---|---|
| [문제해결기법] 5. 욕심쟁이 기법 (0) | 2023.04.17 |
| [문제해결기법] 4. 자료구조2 (0) | 2023.04.16 |
| [문제해결기법] 3. 자료구조1 (0) | 2023.04.16 |
| [문제해결기법] 1. C++ (1) | 2023.04.16 |



