정렬의 최적성
앞에서 우리는 연속한 두 원소를 비교하는 방식으로 정렬하면, O(n2) 보다 좋은 시간 복잡도를 얻을 수 없다는 것을 보였다. 그 다음에 배운 정렬 방식인 퀵정렬, 병합정렬, 힙정렬 에서는 멀리 떨어진 두 원소를 비교하여 교환함으로써 이보다 빠른 시간 복잡도인 O(n log n) 시간을 얻을 수 있었다. 그렇다면 이제 우리가 다시 비슷한 질문을 해보자. O(n log n)보다 더 빠르게 정렬을 수행할 수 있겠는가?
정리.
두 원소를 비교하여 교환하는 방식으로는 O(n log n)보다 더 빠르게 정렬을 수행할 수 없다.
증명.
의사 결정 트리(decision tree)는 어떤 문제에 대해서 판단을 내리는 과정을 트리로 표현한 것이다. 루트는 문제를 풀기 위해서 처음 시작하는 지점이다. 루트를 포함한 중간 노드들은 문제를 해결하는 과정에서 만나는 선택이다. 이 결과에 따라 자식들 중 하나로 이동한다. 판단이 끝나고 결론이 나면 더 이상 결정할 것이 없기 때문에 리프 노드에 해당한다.
아래 그림은 서로 다른 세 수 x1, x2, x3을 정렬하는 과정을 의사결정트리로 표현한 것이다. 일단 두 수를 골라서 비교해야 하므로 x1, x2를 비교한다고 치자. 트리의 루트 노드가 이에 해당한다. 이 결과에 따라, x1 < x2라면 x2와 x3을 비교하자. (왼쪽 자식) 만약 x2 < x3이라면, 두 결과로부터 x1 < x2 < x3임을 알 수 있다. 만약 그렇지 않고 x2 > x3이라면, x2가 가장 큰 수임은 알 수 있지만 x1과 x3의 대소 관계는 아직 알 수 없다. 따라서 x1과 x3을 비교하면, 그 결과에 따라 x1 < x3 < x2인지, x3 < x1 < x2인지를 알 수 있다.
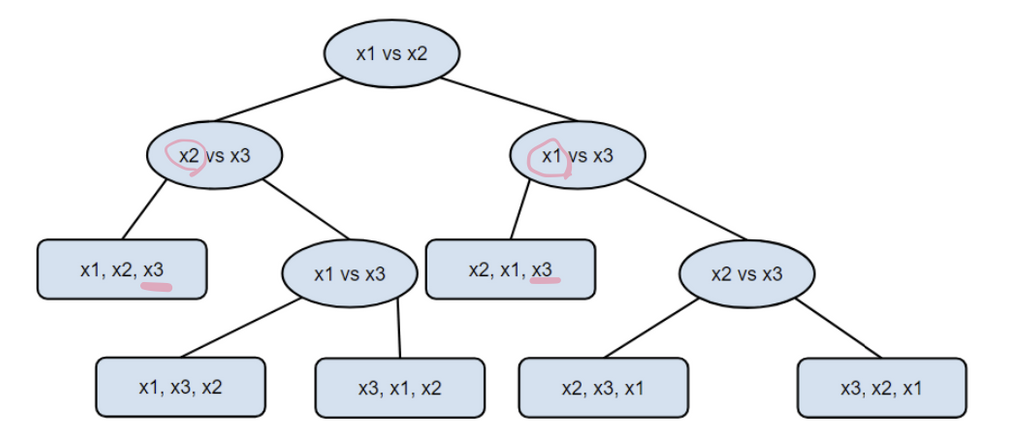
3개의 수를 정렬하는 가짓수는 6개가 있고, 6개의 리프가 가능한 경우에 대응함을 알 수 있다.
그렇다면, 이 트리의 높이, 즉 루트에서 가장 먼 리프까지의 거리가 최악의 경우의 비교 횟수에 대응함을 알 수 있다.
이 높이를 h라고 하자.
높이가 h인 이진 트리의 리프 최대 갯수는 2^h이다.
n개의 수를 정렬했을 때 가능한 경우의 수 (= 의사 결정 트리의 리프의 개수)는 n!이고, 2^h ≥ n! 이 성립한다.
양변에 밑이 2인 로그를 취하면 부등호의 방향이 바뀌지 않으므로 h ≥ log (n!).
log (n!) = log n + log (n-1) + ... + log (n/2) + ... + log 1 ≥ log n + log (n-1) + ... + log (n/2)
≥ log (n/2) + log (n/2) + ... log (n/2) (→ n/2번만큼)
= (n/2)* log(n/2)
= 1⁄2 n(log n - log 2) = 1⁄2 n log n - 1⁄2 log 2
1⁄2 log 2은 n이 2보다 크면 1⁄4 n log n 보다 확실히 작을 것이므로,
h = log(n!) ≥ 1⁄2 n log n - 1⁄2 log 2 ≥ 1⁄4 n log n
임을 알 수 있다. 따라서 의사 결정 트리의 높이는 n log n의 상수배보다 항상 같거나 크다. ( O(n log n) )
출처 : 한국항공대학교 ㅇㅇㅂ교수님 강의자료
'📚 전공 공부 > 알고리즘 해석 및 설계' 카테고리의 다른 글
| [알고리즘] DP - 계단 오르기(cpp) (0) | 2023.04.11 |
|---|---|
| [알고리즘] Greedy algorithm - 이집트 나눗셈(cpp) (0) | 2023.02.09 |
| [알고리즘] 비교기반 정렬의 한계/비교에 기반하지 않은 정렬 (0) | 2023.01.16 |
| [알고리즘] 비교 기반 정렬 문제 (0) | 2023.01.16 |
| [알고리즘] 점화식의 이해(recurrence relation) (0) | 2023.01.16 |



