알고리즘의 정의 : 어떤 입력에도 정확한 출력을 유한한 시간 안에 내는 프로그램
- 어떤 입력 : 문제의 난이도나, 입력의 크기에 상관없이 문제를 풀 수 있다.
- 정확한 출력 : 문제가 요구하는 조건을 만족한다.
- 정답이 요구하는 조건이 무엇인지 명시할 수 있다.
- 유한한 시간 : 무한루프에 빠지지 않고 납득할 수 있는 시간에 종료한다.
ex) 100명의 학생들의 시험 점수 중 최댓값을 구하시오.
- 수학적 귀납법→ 정확성 : 자명하다.
- → 시간 : n명의 점수를 읽으면, n-1번 비교.
- → max(지금까지의 최댓값, i+1번째 학생의 점수)
ex) 100명의 학생들의 시험 점수 중 최빈값을 구하시오.

ex) 입력 : U={1,2, … , n} 중에서 특정한 수 하나만 빼고 무작위의 순서로 n-1개의 숫자가 한번에 하나씩 입력됨.
출력 : U에서 빠진 하나의 수를 찾는다.
- 크기 n인 배열 A를 만들고 0으로 초기화
- 필요한 공간 : 배열 A[n]
- 필요한 시간(비교 횟수) : Best = 1, Worst = n (빠진 수가 n일 때), 평균 n/2
- 숫자 k가 들어오면 A[k] = 1, n-1개의 숫자가 들어온 뒤 A를 처음부터 뒤져서 A[j]=0인 j인덱스를 찾는다.
- 변수 x를 0으로 초기화n-1개의 숫자를 입력받으면, { n(n-1)/2 } - x로 빠진 숫자를 구할 수 있다. (1부터 n까지의 총합에서 x를 빼기)
- 필요한 공간 : 변수 x (n(n-1)/2까지 저장할 수 있는 크기)
- 필요한 시간 : 별도의 추가 검색 시간이 필요없음, 저장소를 이용하여 작업하려면 먼저 이 내용을 복사해야함
- 숫자 k를 입력받을 때마다 x = x+k
→ 문제의 변형과 알고리즘 수정
ex) 입력 : U={1,2, … , n} 중에서 특정한 수 2개만 빼고 무작위의 순서로 n-2개의 숫자가 한번에 하나씩 입력됨.
출력 : U에서 빠진 두 수를 찾는다.
- 크기 n인 배열을 만들어서 빈 인덱스를 찾기
- 변경사항 → 각 수의 합 x와 각 수의 제곱의 합 y도 구한다.
- u + v = n(n+1)/2 - x
- (u^2 + v^2) = n(n+1)(2n+1)/6 - y
- t^2 - (u+v)t + uv = 0의 두 근이 정답이다.
- 미지의 수가 u와 v라고 할 때,
ex) 하노이 탑. 기둥 1의 원반 n개를 어떻게 규칙을 만족하면서 기둥 3으로 모두 옮길 것인가?
→ 알고리즘 설계 기법 중 되부름(recursion) 이용하기.
- n = 1 일 때 옮길 수 있다.
- n = k 일 때 옮길 수 있다고 가정한다.
- n = k+1 일 때 위 가정을 이용하여 k개의 원반을 기둥2로 옮긴다.
- k+1번째 원반을 기둥 3으로 옮긴다.
- 그럼 k개의 원반을 기둥 3으로 옮길 수 있다.
→ k개의 원반을 옮기는 문제 = k-1개의 원반을 옮기는 문제
같은 문제이지만 입력의 크기를 줄일 수 있고, 쉽게 풀 수 있을 때까지 문제의 크기를 줄이면 된다.
→ 원반의 이동 횟수
- n개의 원반이 있을 때 원반의 이동 횟수 T(n) : T(n-1) + 1 + T(n-1) = 2T(n-1) + 1
- T(n) = 2^n - 1
ex) Stable Marriage
→ n명의 남자와 n명의 여자가 있을 때, 다음 조건을 만족하도록 모든 남녀를 1:1로 짝지을 수 있는가?
- 모든 남녀는 이성에 대한 1~n등의 선호도가 있다.
- (남,녀)의 쌍이 (a,b)(c,d)가 있는데, b가 a보다 c를 선호하고 c가 d보다 b를 선호하면 이들은 쌍을 깨고 새로운 쌍을 만들게 된다.
이러한 일이 발생하지 않게 하고 싶다.

- 위 알고리즘은 정확하다.
- 수행 과정에서 모든 여성은 반드시 짝을 갖게 되고, 조건 2에 어긋나는 경우는 수행 과정에서 제거된다.
- 위 알고리즘은 반드시 종료한다.
- 남성 기준으로 수행 과정에서 파트너 변경때마다 파트너 선호도 감소. (여성 파트너의 선호도는 증가)
- 따라서, 한 남성이 n번 이상 파트너가 바뀔 수 없다.
- 총 n^2번 이상 파트너가 바뀔 수 없으므로 시간복잡도는 O(n^2).
최적성의 증명
- 모든 알고리즘 중 이보다 더 좋은 시간복잡도를 얻을 수 없음을 증명하는 것.
- 최소한 반드시 이만큼의 일을 해야하므로 더 잘 할 수는 없다는 것을 보인다.
ex1) 정렬되지 않은 배열 E[1 … n] 에서 어떤 값 k가 있는지 찾고, 있다면 그 인덱스를, 없다면 -1를 반환하시오
int index, ans = -1;
for(index = 0; index < n; index++){
if(k == E[index]){
ans = index;
break;
}
}
return ans;
- ex1의 최적성 증명
- 비교를 한번 할 때마다, 원소 하나의 답 여부를 알 수 있다.
- 따라서 총 n번의 비교가 필요하다.
- n번 비교를 하지 않으려면, 정렬을 하거나 다른 비용을 지불해야함.
ex2) 정렬된 배열 E[1 … n] 에서 어떤 값 k가 있는지 찾고, 있다면 그 인덱스를, 없다면 -1를 반환하시오
- E[1], E[b+1], E[2b+1], … 와 k를 비교한다.E[ ib + 1 ] , E[ ib + 2 ], … E[ (i+1)b ]에서 k값을 찾는다.
- 시간복잡도 : Worst = n/b + b 번 비교 (이분탐색보다는 느리지만 구현은 더 쉽다)
- b = $root(n)$일 때, 최솟값 = 2 $root(n)$ = $O(root(n))$
- ex : b=3, 인덱스 1과 4와 7 비교, … 만약 k가 5라면 4≤5<7 이므로 i=2
- E[ ib + 1 ] ≤ k < E[ (i+1)b + 1 ]인 i를 찾는다.
- 이진 탐색T(n) = 1 + T(n/2) = 1 + (1 + T(n/4)) = … = 1+1+…+1+ T(n/2^k) = k + 1 = O(log n) 번 비교
- 즉 알고리즘 1은 최적이 아니다. 이진탐색이 최적일까?
- n = 2^k 로 가정하면,
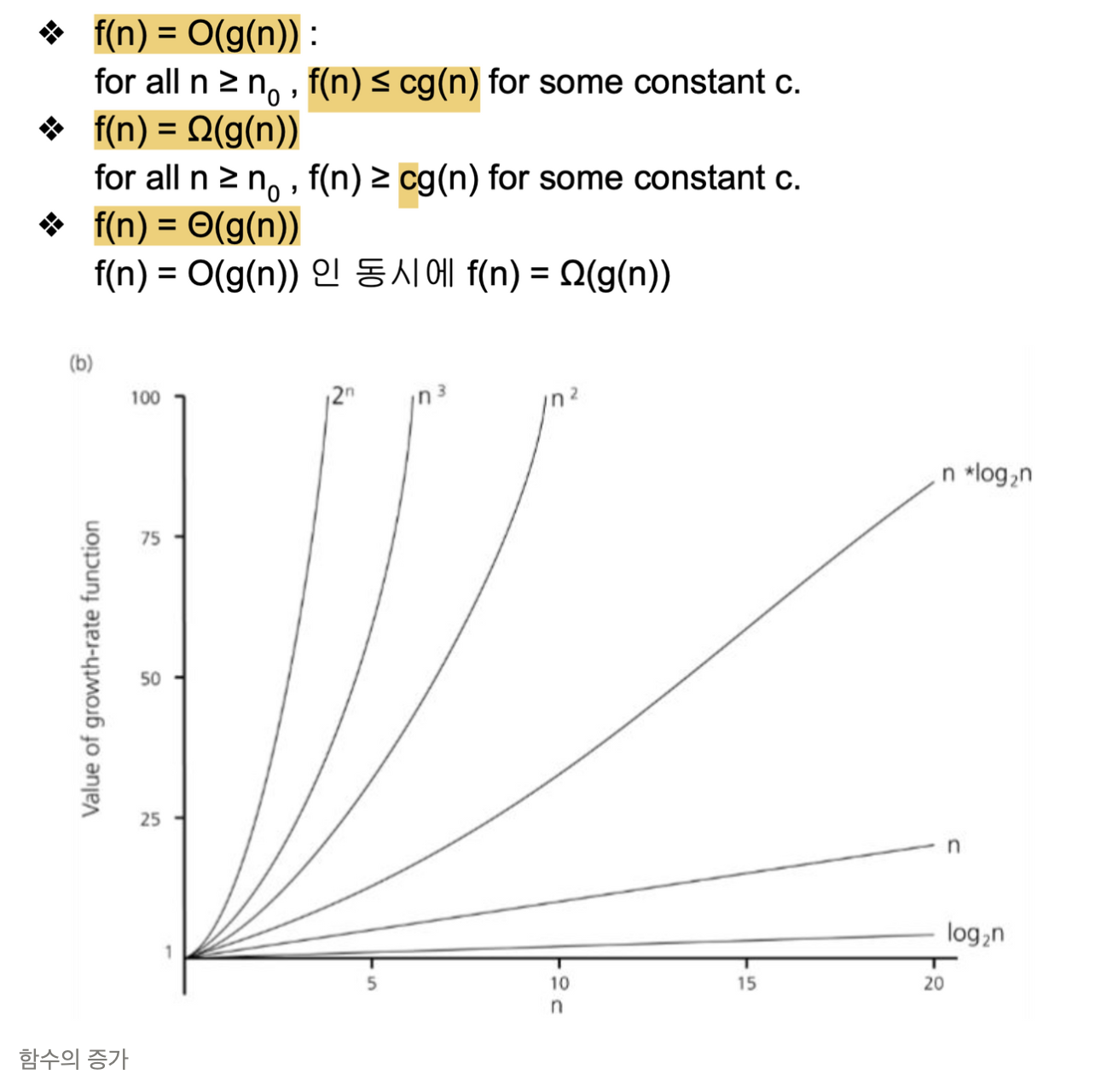
함수의 증가, 시간복잡도
- 우리 알고리즘이 입력이 n개 주어질 때 연산의 개수를 함수 f(n)이라 하자.
- 정의상 f(n)은 자연수에 대해 정의된 함수이다.
- 증가함수일 것이다.
- 그렇다면 f(n)이 n의 증가에 따라 얼마나 빨리 커지는지를 아는 것은 알고리즘 성능 평가에 중요하다.
g(n) = O(f(n)) → g는 f보다 빠르게 증가하지 않는다. (g ≤ f)
'📚 전공 공부 > 알고리즘 해석 및 설계' 카테고리의 다른 글
| [알고리즘] Greedy algorithm - 이집트 나눗셈(cpp) (0) | 2023.02.09 |
|---|---|
| [알고리즘] 정렬의 최적성 (0) | 2023.01.16 |
| [알고리즘] 비교기반 정렬의 한계/비교에 기반하지 않은 정렬 (0) | 2023.01.16 |
| [알고리즘] 비교 기반 정렬 문제 (0) | 2023.01.16 |
| [알고리즘] 점화식의 이해(recurrence relation) (0) | 2023.01.16 |


